РЛЦ коло је електрично коло које се састоји од отпорника, пригушнице и кондензатора и представљени су словима Р, Л и Ц. Резонантни РЛЦ кругови су повезани у серију и паралелно. Назив РЛЦ кола изведен је из почетног слова из компонената отпора, пригушнице и кондензатора. За тренутну намену, коло формира хармонијски осцилатор. Помоћу ЛЦ коло то одзвања. Ако се отпор повећа, он распада осцилације које је познато као пригушивање. Неки отпор је тешко пронаћи у реалном времену, чак и након што отпорник није идентификован као компонента коју решава ЛЦ коло.
Резонантни РЛЦ кругови
Док је реч о резонанци, она је сложена компонента и има доста одступања. Импеданса з и њен круг су дефинисани као
З = Р + ЈКС
Тамо где је Р отпор, Ј је имагинарна јединица, а Кс реактанца.
Постоји импулс потписан између Р и ЈКС. Замишљена јединица је спољни отпор. Складиштена енергија је компонента кондензатор и индуктор. Кондензатори су смештени у електричном пољу, а пригушнице у пољу величине.
САЦ.= 1 / јωц
= -Ј / ωц
САЛ= јωЛ
Из једначине З = Р + ЈК реактанције можемо дефинисати као
ИксЦ.= -1 / ωц
ИксЛ =ωЛ
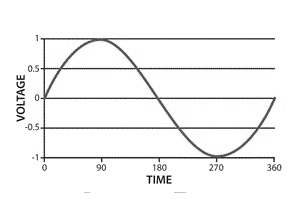
Апсолутна вредност реактанције од индуктор и пуњење кондензатора са фреквенцијом као што је приказано на доњој слици.

К фактор
Скраћеница К је дефинисана као квалитет, а позната је и као фактор квалитета. Фактор квалитета описује недовољно пригушени резонатор. Ако се резонатор премало пригуши, фактор квалитета се смањује. Пригушивање кола електричног резонатора генерише губитак енергије у отпорним компонентама. Математички израз К фактора дефинисан је као
К ( ω ) = максимална ускладиштена енергија енергије / губитак снаге
К фактор се ослања на фреквенцију и најчешће се наводи за резонантну фреквенцију и максималну енергију ускладиштену у кондензатору и индуктору може израчунати резонантну фреквенцију која је ускладиштена у резонантном колу. Релевантне једначине су
Максимална ускладиштена енергија = ЛИдваЛрмс= Ц ВдваЦрмс
ИЛрмс се означавају као ефективна струја кроз индуктор. Једнака је укупној ефективној струји која се формира у колу у серијском колу, а у паралелном колу није једнака. Слично томе, у ВЦрмс је напон на кондензатору, он је приказан у паралелном колу и једнак је ефективном ефективном напону, али у серији је круг договорен разделником потенцијала. Стога је серијско коло једноставно израчунати максималну енергију ускладиштену преко индикатора, а у паралелним круговима се разматра кроз кондензатор.
Стварна снага се дегенерише у отпорнику
П = ВРрмсЈаРрмс= ИдваРрмсР = ВдваРрмс/ Р.
Најлакши начин да пронађете серијски РЛЦ круг
К(С)ω0= ω0 ЈадвармсЛ / ИдвармсР = ω0Л / Р
Паралелни круг треба узети у обзир напон
К(П)ω0= ω0РЦВдваЦрмс/ ВдваЦрмс= ω0ЦР
Серијски РЛЦ круг
Коло РЛЦ серије састоји се од отпора, индуктора и кондензатора који су серијски повезани у серијски РЛЦ круг. Дијаграм испод приказује серијски РЛЦ круг. У овом колу кондензатор и индуктор ће се међусобно комбиновати и повећати фреквенцију. Ако можемо поново повезати Ксцис са негативом, онда је јасно да КСЛ + КСЦ треба да буду једнаки нули за ову специфичну фреквенцију КСЛ = -КСЦимпеданце компоненте имагинарног тачно се међусобно поништавају. При овом кретању фреквенције, импеданса кола има малу величину и фазни угао нула, назива се резонантном фреквенцијом кола.

Серијски РЛЦ круг
ИксЛ+ КсЦ.= 0
ИксЛ= - КсЦ.= ω0Л = 1 / ω0Ц = 1 / ЛЦ
ω0 =√1 / ЛЦω0
= 2Π ф 0
Произвољни РЛЦ круг
Резонантне ефекте можемо посматрати узимајући у обзир напон на отпорним компонентама до улазног напона за пример који можемо узети у обзир за кондензатор.
ВЦ / В = 1/1-ωдваЛЦ + ј ωРЦ
За вредности Р, Л и Ц приказан је однос на основу угаоне фреквенције и слика показује својства појачања. Резонантна фреквенција
ВЦ / В- 1 / ј ω0РЦ
ВЦ / В- ј ω0Л / Р
Видимо да је ово позитивно коло укупна количина расипане снаге константна

Паралелни РЛЦ круг
У паралелном РЛЦ колу отпор компоненте, пригушница и кондензатор су повезани паралелно. Резонантно РЛЦ коло је двоструко серијско коло у улогама размене напона и струје. Стога круг има тренутни добитак, а не импедансу, а појачање напона је максимум на резонантној фреквенцији или је минимизирано. Укупна импеданса кола дата је као

Паралелни РЛЦ круг
= Р ‖ ЗЛ‖ САЦ.
= Р / 1- ЈР (1 / КсЦ.+ 1 / КсЛ)
= Р / 1+ ЈР (ωц - 1 / ωЛ)
Када ИксЦ. = - ИксЛ Резонантни пикови долазе поново и самим тим резонантна фреквенција има исти однос.
ω0 =√1 / ЛЦ
Да би се израчунало струјно појачање гледањем струје у сваком краку, тада је појачање кондензатора дато као
иц/ и = јωРЦ / 1+ јР (ωц - 1 / ωЛ)

Тренутни добитак магнитуде приказан је на слици, а резонантна фреквенција је
иц/ и = јРЦ
Примене резонантних РЛЦ кола
Резонантни РЛЦ кругови имају много примена попут
- Коло осцилатора , радијски пријемници и телевизијски уређаји се користе за подешавање.
- Серијско и РЛЦ коло углавном укључује обраду сигнала и комуникациони систем
- Серијски резонантни ЛЦ круг се користи за повећање напона
- Серија и паралелни ЛЦ круг се користе у индукционом грејању
Овај чланак даје информације о РЛЦ колу, серијама и паралелама РЛЦ кола, К фактору и примени резонантних РЛЦ кола. Надам се да су дате информације у чланку корисне за давање неких добрих информација и разумевање пројекта. Даље, ако имате питања у вези са овим чланком или на електрични и електронски пројекти можете коментарисати у одељку испод. Ево питања за вас, у паралелном РЛЦ колу, која вредност се увек може користити као векторска референца?
Фото кредити: